Difference between revisions of "АЙЛАНА"
| 1 -сап: | 1 -сап: | ||
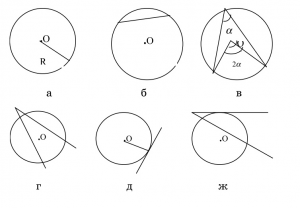
– берилген чекиттен (О борборунан) бирдей алыстыкта жаткан тегиздиктеги ийри сызык. Анын О борбору м‑н анын кандайдыр чекитин туташтыруучу ''R'' кесиндиси А‑нын радиусу (а, сүрөт). А‑нын эки чекитин туташтырган кесинди хорда ''(б,'' сүрөт), борбору аркылуу өткөн эң узун хорда диаметр деп аталат. Хордага перпендикуляр болгон диаметр аны тең 2ге бөлөт. Жалпы чекитке ээ болуп, эки хордадан пайда болгон бурч ичтен сызылган бурч. Чокусу А‑нын борборунда жаткан бурч борб. бурч ''(в,'' сүрөт). Ичтен сызылган бурч жаанын жарымы м‑н өлчөнөт ж‑а ошол эле жааны камтыган борб. бурчтун жарымына барабар (в, сүрөт). Кесүүчү эки түз сызык аркылуу пайда болгон бурч анын эки жагы аркылуу чектелген жаанын жарым айырмасы аркылуу өлчөнөт ''(г,'' сүрөт). А‑дагы чекит аркы- | – берилген чекиттен (О борборунан) бирдей алыстыкта жаткан тегиздиктеги ийри сызык. Анын О борбору м‑н анын кандайдыр чекитин туташтыруучу ''R'' кесиндиси А‑нын радиусу (а, сүрөт). А‑нын эки чекитин туташтырган кесинди хорда ''(б,'' сүрөт), борбору аркылуу өткөн эң узун хорда диаметр деп аталат. Хордага перпендикуляр болгон диаметр аны тең 2ге бөлөт. Жалпы чекитке ээ болуп, эки хордадан пайда болгон бурч ичтен сызылган бурч. Чокусу А‑нын борборунда жаткан бурч борб. бурч ''(в,'' сүрөт). Ичтен сызылган бурч жаанын жарымы м‑н өлчөнөт ж‑а ошол эле жааны камтыган борб. бурчтун жарымына барабар (в, сүрөт). Кесүүчү эки түз сызык аркылуу пайда болгон бурч анын эки жагы аркылуу чектелген жаанын жарым айырмасы аркылуу өлчөнөт ''(г,'' сүрөт). А‑дагы чекит аркы- | ||
[[File:АЙЛАНА56.png | thumb | none]] | [[File:АЙЛАНА56.png | thumb | none]] | ||
луу бир гана жаныма жүргүзүүгө болот. Бул жаныма ал чекит аркылуу жүргүзүлгөн радиуска перпендикуляр (''д,'' сүрөт). Эгер А‑нын сыртында жаткан М чекити аркылуу ага карата кесүүчү түз сызык жүргүзүлсө, анда М чекитинен А‑ны кесүүчү чекиттерге чейинки аралыктардын көбөйтүндүсү М чекитинен А‑га чейинки жаныманын уз‑нун квадратына барабар (ж, сүрөт). А‑нын уз‑нун анын диаметрине болгон катышы бардык А‑лар үчүн бирдей. Бул катыш трансценденттик сан ж‑а гр. «л» тамгасы м‑н белгиленет, сан мааниси я =3,614159... А‑нын уз. '' | луу бир гана жаныма жүргүзүүгө болот. Бул жаныма ал чекит аркылуу жүргүзүлгөн радиуска перпендикуляр (''д,'' сүрөт). Эгер А‑нын сыртында жаткан М чекити аркылуу ага карата кесүүчү түз сызык жүргүзүлсө, анда М чекитинен А‑ны кесүүчү чекиттерге чейинки аралыктардын көбөйтүндүсү М чекитинен А‑га чейинки жаныманын уз‑нун квадратына барабар (ж, сүрөт). А‑нын уз‑нун анын диаметрине болгон катышы бардык А‑лар үчүн бирдей. Бул катыш трансценденттик сан ж‑а гр. «л» тамгасы м‑н белгиленет, сан мааниси я =3,614159... А‑нын уз. ''= 2nR.'' Тегиздиктин А. м‑н чектелген ж‑а анын борборунун камтыган бөлүгү ''тегерек'' деп аталат. Декарттык тик бурчтуу координаталар системасында А‑нын теңдемеси ''(х – а)<sup>1</sup> + (у – Vf = R<sup>2'' түрүндө жазылат, мында ''а'' ж‑а ''Ь –'' берилген А‑нын борборунун координаталары. | ||
''Б .Э. Канетов.''<br> | ''Б .Э. Канетов.''<br> | ||
13:44, 25 -октябрь (Тогуздун айы) 2022 -деги абалы
– берилген чекиттен (О борборунан) бирдей алыстыкта жаткан тегиздиктеги ийри сызык. Анын О борбору м‑н анын кандайдыр чекитин туташтыруучу R кесиндиси А‑нын радиусу (а, сүрөт). А‑нын эки чекитин туташтырган кесинди хорда (б, сүрөт), борбору аркылуу өткөн эң узун хорда диаметр деп аталат. Хордага перпендикуляр болгон диаметр аны тең 2ге бөлөт. Жалпы чекитке ээ болуп, эки хордадан пайда болгон бурч ичтен сызылган бурч. Чокусу А‑нын борборунда жаткан бурч борб. бурч (в, сүрөт). Ичтен сызылган бурч жаанын жарымы м‑н өлчөнөт ж‑а ошол эле жааны камтыган борб. бурчтун жарымына барабар (в, сүрөт). Кесүүчү эки түз сызык аркылуу пайда болгон бурч анын эки жагы аркылуу чектелген жаанын жарым айырмасы аркылуу өлчөнөт (г, сүрөт). А‑дагы чекит аркы-
луу бир гана жаныма жүргүзүүгө болот. Бул жаныма ал чекит аркылуу жүргүзүлгөн радиуска перпендикуляр (д, сүрөт). Эгер А‑нын сыртында жаткан М чекити аркылуу ага карата кесүүчү түз сызык жүргүзүлсө, анда М чекитинен А‑ны кесүүчү чекиттерге чейинки аралыктардын көбөйтүндүсү М чекитинен А‑га чейинки жаныманын уз‑нун квадратына барабар (ж, сүрөт). А‑нын уз‑нун анын диаметрине болгон катышы бардык А‑лар үчүн бирдей. Бул катыш трансценденттик сан ж‑а гр. «л» тамгасы м‑н белгиленет, сан мааниси я =3,614159... А‑нын уз. = 2nR. Тегиздиктин А. м‑н чектелген ж‑а анын борборунун камтыган бөлүгү тегерек деп аталат. Декарттык тик бурчтуу координаталар системасында А‑нын теңдемеси (х – а)1 + (у – Vf = R2 түрүндө жазылат, мында а ж‑а Ь – берилген А‑нын борборунун координаталары.
Б .Э. Канетов.