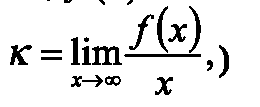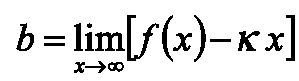Difference between revisions of "АСИМПТОТА"
Jump to navigation
Jump to search
| 7 -сап: | 7 -сап: | ||
'''b = lim<sub>x→∞</sub> [f(x) – kx]'''<br><br> | '''b = lim<sub>x→∞</sub> [f(x) – kx]'''<br><br> | ||
[[File:АСИМПТОТА_87.png | thumb | Формула 2]]<br> | [[File:АСИМПТОТА_87.png | thumb | Формула 2]]<br> | ||
түз сызыгы жантык А. | түз сызыгы жантык А. деп аталат. 2-тартиптеги ийри сызыктардан ''гипербола'' гана А-га ээ болот. Математикалык анализде А. түшүнүгү чоң мааниге ээ.<br>''Ад.: Кудрявцев JI. Д.'' Математический анализ в двух томах. М., 1980. ''Б.'' | ||
чоң мааниге ээ.<br>''Ад.: Кудрявцев JI. Д.'' Математический анализ в двух | |||
томах. М., 1980. ''Б.'' | |||
''Э.Назаркулова.''<br> | ''Э.Назаркулова.''<br> | ||
11:03, 23 -октябрь (Тогуздун айы) 2023 -деги абалы
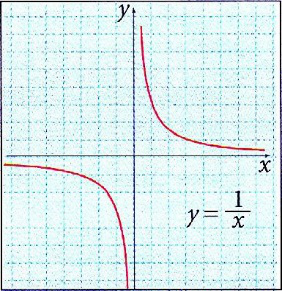
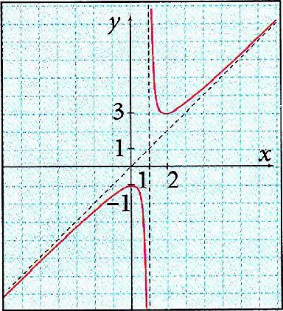
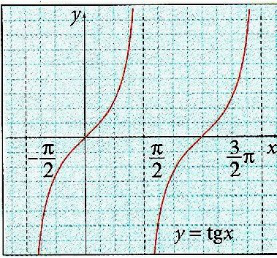
АСИМПТОТА (гр. asymptotes – дал келбөөчү) - координаталар башталмасынан чексиз алыста-
ган сайын ийри сызыкка чексиз жакындай берген түз сызык. А үч түргө бөлүнөт: 1.
|х| → ∞, у→а болгондо у = а түз сызыгы – горизонталь А.; 2.
х —> b , |у| —> ∞ болгондо х = b түз сызыгы – вертикаль А.; 3.
х → ∞. f(x) → ∞ болгондо у = кх + Ь ( мында )
b = limx→∞ [f(x) – kx]
түз сызыгы жантык А. деп аталат. 2-тартиптеги ийри сызыктардан гипербола гана А-га ээ болот. Математикалык анализде А. түшүнүгү чоң мааниге ээ.
Ад.: Кудрявцев JI. Д. Математический анализ в двух томах. М., 1980. Б.
Э.Назаркулова.