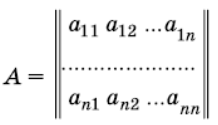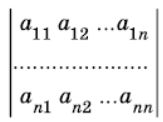АНЫКТАГЫЧ
АНЫКТАГЫЧ , детерминант — n — тартиптеги квадраттык А= ||aij|| матрицасынын
(-1)ta1i1 түрүндөгү мүчөлөрүнүн суммасы,
мында iti2,..., in – 1, 2, ..., п сандарынын орундаштыруусу, t – орундаштыруунун инверсияларынын саны. Берилген Failed to parse (syntax error): {\displaystyle Формула 2 }
матрицасынын аныктагычы же Failed to parse (syntax error): {\displaystyle Формула 3}
, же det А деп белгиленет. А матрицасынын аныктагычы
n! мүчөлөрдөн турат:
п = 1 болсо, det А '= ап, п'=2
болсо, det А =' а 11а 22 -а 21а 12 болот. А матрицасынын аныктагычын, анын сапчаларына көз
каранды функция түрүндө караса ьщгайлуу:
det А '= D(a1 Анда d:Mn->i2(A->detA) ча-
гылдыруусу төмөнкү үч шартты канааттандырат: 1) d(A') деген А матрицасынын каалагандай сапчаларынын сызыктуу функциясы:
£>(<*! Аа. + ап) = XD(a1 а. ап)+
+/±D(a1 6. ап), мында X, цеД; 2) эгер А
матрицасынын а1 сапчасын а1+ а1 сапчасына i*j
алмаштыруу аркылуу В матрицасын алсак,
анда d'(A) = d(B); 3) d(En) = 1. Жогорку R – чыныгы сандардын көптүгү, Мп – бардык п – тартиптеги квадраттык матрицалардын жыйындысы, Еп – бирдик матрица. 1-3 шарттары d чагылдыруусун аныктайт, б. а. эгер d:Mn(R) ->Д чагылдыруусу 1–3 шарттарын канааттандырса,
анда d(A)=detA. Ушундай жол м-н A-тар аксиоматика түрүндө аныкталат.
Ад.: Курош А. Г. Курс высшей алгебры. М., 1975;
Кострикин А. И'. Введение в алгебру. М.,1977.
А. А. Чекеев, С. Токсонбаев.