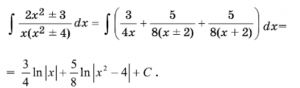АНЫКТАЛБАГАН КОЭФФИЦИЕНТТЕР МЕТОДУ

АНЫКТАЛБАГАН КОЭФФИЦИЕНТТЕР МЕТОДУ – туюнтманын жалпы түрү алдын ала белгилүү болгон учурдагы анын белгисиз коэффтерин табуу ыкмасы. Р(х) ж-а Q(x) алг. көп мүчөлөрдөн турган Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle {P(x) \over Q(x)}} түрүндөгү дурус бөлчөгүн (алымынын даражасы бөлүмүнүкүнөн кичине) чектүү сандагы жөнөкөй бөлчөктөрдүн суммасы Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle {A \over {(x-a)^k}}; {{Bx+C } \over {(x^2 + px +q)^k}}; (k = 1,2,3...)}

Формула 5

түрүндө туюнтууга болот, мында А,В,С, a,p,q чыныгы сандар ж-а х² + рх + q квадраттык үч мөчүсү чыныгы тамырга ээ болбойт. Мис., Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle {2x^2-3 \over (x(x^2-4)} } рационалдык туюнтмасы Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle {A \over x}+{B \over (x-2)}+{C \over (x+2)} } дөгү бөлчөктөрдүн суммасына ажырайт. А, В, Сны табуу үчүн эки туюнтманы барабарлап Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle {(2x^2-3) \over x(x^2-4)} ={A \over x} + {B\over (x-2)}+{C \over (x+2)} } , жалпы бөлүмдөн кутулуп, окшош мүчөлөрүн топтоп, жөнөкөйлөштүргөндөн кийин 2х² - 3 = (А + В + С)х²+ 2(В -С)х - 4А түрүнө келет. Бул барабардык x тин бардык маанилеринде туура, ошондуктан х тин бирдей даражага ээ болгон мүчөлөрүнүн коэффтери барабар болот. Анда:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \begin{cases} A+B+C \\ 2(B-C) =0 \\ -4A=-3 \end{cases}}

Формула 6.1

системасын чыгарып А = 3/4, В = 5/8, С = 5/8 маанилерин табууга болот. Берилген туюнтманын ажыратылып жазылышы:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle {(2x^2-3) \over x(x^2-4)} ={3 \over 4x} + {5 \over 8(x-2)}+{5 \over 8(x+2)} }

Формула 6

А.к.м. дифференциалдык теңдемелерди чыгарууда, рационал­дык функцияларды интегралдоодо, көп мүчөнү көбөйтүүчүлөргө ажыратууда, сандык методдордо ж. б. маселелерде кеңири колдонулат. Мис.,

${\textstyle \int {(2x^{2}-3) \over x(x^{2}-4)}dx}$

Формула 7

интегралынын жогоркудай ажыралышы пайдаланылганда, төмөнкүдөй интегралданат:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \int {(2x^2-3) \over x(x^2-4)} dx = \int \bigl({{3\over 4x} + {4 \over 8(x\pm2)}+{5\over 8(x+2)}}\bigr)dx = {3 \over 4} \ln \left\vert x \right\vert + {5\over 8} \ln \left\vert x^2-4 \right\vert + C }

Формула 8

Ад.: Фихтенголъц Г. М. Курс дифференциального и интегрального исчисления. Т. 2.М., 1969; Смирнов В. И. Курс высшей математики. М., 1974.
Б. Э. Назаркулова.