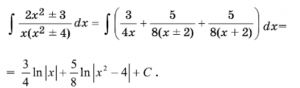АНЫКТАЛБАГАН КОЭФФИЦИЕНТТЕР МЕТОДУ

 – туюнтманын жалпы түрү алдын ала белгилүү болгон учурдагы анын белгисиз коэффтерин табуу ыкмасы. Р(х) ж-а Q(x) алг. көп мүчөлөрдөн турган

$Q(x)/P(x)$ түрүндөгү дурус бөлчөгүн (алымынын даражасы бөлүмүнүкүнөн кичине) чектүү сандагы жөнөкөй бөлчөктөрдүн суммасы
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Формула 5}}

Формула 5

түрүндө туюнтууга болот, мында А,В,С, a,p,q чыныгы сандар ж-а х² + рх + q квадраттык үч мөчү сү чыныгы тамырга ээ болбойт. Мис.,
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <br> 2x^2-3/(x(x^2-4)<br> }
рационалдык туюнтмасы
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <br> A/x+B/(x-2)+C/(x+2)<br> }
дөгү бөлчөктөрдүн суммасына ажырайт. А, В, Сны табуу үчүн эки туюнтманы барабарлап
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <br> (2x^2-3)/x(x^2-4) =A/x+B/(x-2)+C/(x+2)<br> }
ЖалПЫ 6ӨЛҮМДӨН Ку-
тулуп, окшош мүчөлөрүн топтоп, жөнөкөйлөштүргөндөн кийин 2х² -3 = (А + В + С)х²+ 2(В -С)х - 4А түрүнө келет. Бул барабардык хтин бардык маанилеринде туура, ошондуктан х тин бирдей даражага ээ болгон мүчөлөрүнүн коэфф-
тери барабар болот. Анда:
${\text{Формула 6.1}}$

Формула 6.1

системасын чыгарып А = 3/4, В' = 5/8, С = 5/8 маанилерин табууга болот. Берилген туюнтманын ажыратылып жазылышы:Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Формула 6}

Формула 6

А.к.м. дифференциалдык теңдемелерди чыгарууда, рационал­дык функцияларды интегралдоодо, көп мүчөнү көбөйтүүчүлөргө ажыратууда, сандык методдордо ж. б. маселелерде кеңири колдонулат. Мис., :Failed to parse (syntax error): {\displaystyle Формула 7 }

Формула 7

интегралынын жогоркудай ажыралышы пайдаланылганда, төмөнкүдөй интегралданат: :Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Формула 8}

Формула 8

Ад.: Фихтенголъц Г. М. Курс дифференциального и интегрального исчисления. Т. 2.М., 1969; Смирнов В. И. Курс высшей математики. М., 1974.
Б. Э. Назаркулова.