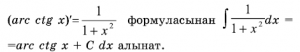Difference between revisions of "АНЫКТАЛБАГАН ИНТЕГРАЛ"
м (1 версия) |
(formula edit done) |
||
| 1 -сап: | 1 -сап: | ||
– белгилүү аймакта берилген ''f(x)'' функциясынын бардык | |||
''F(x)+C'' түрүндөгү баштапкы функцияларынын<br> | ''F(x)+C'' түрүндөгү баштапкы функцияларынын<br> | ||
жыйындысы. Ал ∫ ''f(x)dx'' символу м-н белгиле-<br> | жыйындысы. Ал ∫ ''f(x)dx'' символу м-н белгиле-<br> | ||
нет ж-а ∫ ''f(x)dx=F(x)+C'' (1) түрүндө жазылат,<br> | нет ж-а ∫ ''f(x)dx=F(x)+C'' (1) түрүндө жазылат,<br> | ||
мында ∫ – интеграл белгиси, ''f(x)'' интеграл ас-<br> | мында ∫ – интеграл белгиси, ''f(x)'' интеграл ас-<br> | ||
тындагы функция, ∫ ''f(x)dx —'' интеграл астындагы туюнтма, ''F(x)'' функциясы ''f(x)'' функциясынын баштапкы функциясы, С – турактуу чоңдук. Баштапкы функциялардын ичинен кайсынысын алуу белгисиз (б. а. С аныкталбаган) болгондуктан жогорку (1) интеграл А. и. | тындагы функция, ∫ ''f(x)dx —'' интеграл астындагы туюнтма, ''F(x)'' функциясы ''f(x)'' функциясынын баштапкы функциясы, С – турактуу чоңдук. Баштапкы функциялардын ичинен кайсынысын алуу белгисиз (б. а. ''С'' аныкталбаган) болгондуктан жогорку (1) интеграл А. и. | ||
деп аталат. Интеграл астындагы туюнтманы | деп аталат. Интеграл астындагы туюнтманы | ||
''f(x)dx=dF(x'''' | ''f(x)dx=dF(x''')''''' түрүндө да жазууга болот (к. ''Интеграл, Интегралдык эсептөөлөр).'' Берилген | ||
функциянын А. и-ын аныктоо амалы дифференциалдоо амалына тескери болуп, ал интегралдоо деп аталат. Туундунун ''F '(x)=f(x)'' формуласынан (1) формула келип чыгат. Алсак, <math> | функциянын А. и-ын аныктоо амалы дифференциалдоо амалына тескери болуп, ал интегралдоо деп аталат. Туундунун ''F '(x)=f(x)'' формуласынан (1) формула келип чыгат. Алсак, | ||
<math> (arc \quad ctg \quad x)'={1 \over {1+x^2}} \quad | |||
\text{формуласынан} </math> | |||
<math> \int {1 \over {1+x^2}}dx = | |||
arc \quad ctg \quad x + C \quad dx \quad \text{алынат} </math> | |||
[[File:АНЫКТАЛБАГАН ИНТЕГРАЛ_8.png | thumb | Формула 4]] | [[File:АНЫКТАЛБАГАН ИНТЕГРАЛ_8.png | thumb | Формула 4]] | ||
Ад.: ''Бермант А. Ф., Арамонович И. Г.'' Краткий | Ад.: ''Бермант А. Ф., Арамонович И. Г.'' Краткий | ||
курс математического анализа. М., 1973; ''Кудрявцев'''' | курс математического анализа. М., 1973; ''Кудрявцев'''' | ||
Л. Д..'' Математический анализ в двух томах. М., 1980.<br> | |||
''Б. Э. Назаркулова.''<br> | ''Б. Э. Назаркулова.''<br> | ||
21:16, 14 -ноябрь (Жетинин айы) 2022 -деги абалы
– белгилүү аймакта берилген f(x) функциясынын бардык
F(x)+C түрүндөгү баштапкы функцияларынын
жыйындысы. Ал ∫ f(x)dx символу м-н белгиле-
нет ж-а ∫ f(x)dx=F(x)+C (1) түрүндө жазылат,
мында ∫ – интеграл белгиси, f(x) интеграл ас-
тындагы функция, ∫ f(x)dx — интеграл астындагы туюнтма, F(x) функциясы f(x) функциясынын баштапкы функциясы, С – турактуу чоңдук. Баштапкы функциялардын ичинен кайсынысын алуу белгисиз (б. а. С аныкталбаган) болгондуктан жогорку (1) интеграл А. и.
деп аталат. Интеграл астындагы туюнтманы
f(x)dx=dF(x) түрүндө да жазууга болот (к. Интеграл, Интегралдык эсептөөлөр). Берилген
функциянын А. и-ын аныктоо амалы дифференциалдоо амалына тескери болуп, ал интегралдоо деп аталат. Туундунун F '(x)=f(x) формуласынан (1) формула келип чыгат. Алсак,
Ад.: Бермант А. Ф., Арамонович И. Г. Краткий
курс математического анализа. М., 1973; Кудрявцев''
Л. Д.. Математический анализ в двух томах. М., 1980.
Б. Э. Назаркулова.