Difference between revisions of "АЯНТ (геометрия)"
Jump to navigation
Jump to search
556-684>KadyrM |
|||
| 1 -сап: | 1 -сап: | ||
г е о м е т р и я д а ‒ 1) геом. фигуралар м-н беттердин сандык мүнөздөмөлөрүнүн бири. А. төмөнкү касиеттерге ээ: 1) терс эмес; 2) аддитивдүү; 3) жылдырууда сакталат; 4) бирдик квадраттын А-ы 1ге барабар. А-ты эсептөө байыртадан эле геометриянын негизги | г е о м е т р и я д а ‒ 1) геом. фигуралар м-н беттердин сандык мүнөздөмөлөрүнүн бири. А. төмөнкү касиеттерге ээ: 1) терс эмес; 2) аддитивдүү; 3) жылдырууда сакталат; 4) бирдик квадраттын А-ы 1ге барабар. А-ты эсептөө байыртадан эле геометриянын негизги маселелеринин бири болгон. Байыркы грек окумуштуулары айрым фигуралардын А-тарын эсептөөнүн эрежелерин билишкен. Бул эрежелер Евклиддин «Башталыштар» аттуу жыйнагында теорема формасында берилген. Тегиздиктеги көп бурчтуктардын А-тары көп бурчтуктарды тик бурчтуктарга келтирүү аркылуу ченелет. Айрым А-тарды Кавальери принцибинин жардамы м-н аныктоого болот. Ар кандай жалпак фигуралардын А-тары аныкталган интегралдын жардамы м-н эсептелинет. Мис., төмөн жагынан (''а,'' 0) ж-а (''b,'' 0) арасындагы ''O<sub>x'' огунун кесиндиси м-н чектелген, ал эми жогору жагынан терс эмес ж-а [''a, b''] сегментинде аныкталган үзгүлтүксүз ''f(x'') функциясы м-н чектелген фигуранын А-ты кара <math>S=\int_a^b f(x)\,dx<br> | ||
</math> | |||
''f(x'') функциясы м-н чектелген фигуранын А-ты кара <math>S=\int_a^b f(x)\,dx<br> | |||
</math> | |||
[[File:АЯНТ 189.png | thumb | Сүр.1]] | [[File:АЯНТ 189.png | thumb | Сүр.1]] | ||
[[File:АЯНТ 190.png | thumb | none]] | [[File:АЯНТ 190.png | thumb | none]] | ||
| 18 -сап: | 16 -сап: | ||
a b<br> | a b<br> | ||
X''<br> | X''<br> | ||
14:03, 4 Август (Баш оона) 2022 -деги абалы
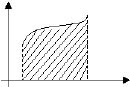
г е о м е т р и я д а ‒ 1) геом. фигуралар м-н беттердин сандык мүнөздөмөлөрүнүн бири. А. төмөнкү касиеттерге ээ: 1) терс эмес; 2) аддитивдүү; 3) жылдырууда сакталат; 4) бирдик квадраттын А-ы 1ге барабар. А-ты эсептөө байыртадан эле геометриянын негизги маселелеринин бири болгон. Байыркы грек окумуштуулары айрым фигуралардын А-тарын эсептөөнүн эрежелерин билишкен. Бул эрежелер Евклиддин «Башталыштар» аттуу жыйнагында теорема формасында берилген. Тегиздиктеги көп бурчтуктардын А-тары көп бурчтуктарды тик бурчтуктарга келтирүү аркылуу ченелет. Айрым А-тарды Кавальери принцибинин жардамы м-н аныктоого болот. Ар кандай жалпак фигуралардын А-тары аныкталган интегралдын жардамы м-н эсептелинет. Мис., төмөн жагынан (а, 0) ж-а (b, 0) арасындагы Ox огунун кесиндиси м-н чектелген, ал эми жогору жагынан терс эмес ж-а [a, b] сегментинде аныкталган үзгүлтүксүз f(x) функциясы м-н чектелген фигуранын А-ты кара
интегралы м-н туюнтулат (к. сүрөт).
Көп грандыктын бетинин А-ы анын грандары нын А-тарынын суммасына барабар.
=(u, n) теӊдемеси м-н берилген D бетинин туюк аймагынын аянты төмөнкү формула м-н эсеп-
телет:
,мында
ал эми rи ж-а rn болсо и ж-а n б-ча алынган жекече туундулар болот. Б. Э. Канетов.
Ю
a b
X