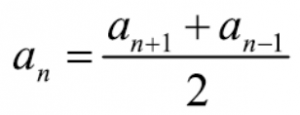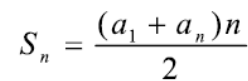Difference between revisions of "АРИФМЕТИКАЛЫК ПРОГРЕССИЯ"
Jump to navigation
Jump to search
| 1 -сап: | 1 -сап: | ||
'''АРИФМЕТИКАЛЫК''' (лат. progressio – өсүү) – сан удаалаштыгы, анын ар бир кийинки мүчөсү мурдакысына А. п-нын айырмасы деп аталган, кандайдыр ''d'' турактуу с анын кошуу м-н алынган сан катары. Ap бир А. п. . ''a,a+d,a+2d,a+3d,...'' түрүндө жазылат, жалпы мүчөсү а<sub>п</sub> = ''а + '(п'' -l) d. А. п-ны мүнөздөөчү формула '''<br>'''<br> | '''АРИФМЕТИКАЛЫК''' '''ПРОГРЕССИЯ ('''лат. progressio – өсүү) – сан удаалаштыгы, анын ар бир кийинки мүчөсү мурдакысына А. п-нын айырмасы деп аталган, кандайдыр ''d'' турактуу с анын кошуу м-н алынган сан катары. Ap бир А. п. . ''a,a+d,a+2d,a+3d,...'' түрүндө жазылат, жалпы мүчөсү а<sub>п</sub> = ''а + '(п'' -l) d. А. п-ны мүнөздөөчү формула :'''<br>'''<br> | ||
[[File:АРИФМЕТИКАЛЫК ПРОГРЕССИЯ_61.png | thumb | Формула 12]] | [[File:АРИФМЕТИКАЛЫК ПРОГРЕССИЯ_61.png | thumb | Формула 12]] | ||
Эгер ''d''>0 болсо, анда А. п. өсүүчү, эгер ''d''<0 болсо, кемүүчү деп аталат. А. п-нын эң жөнөкөй мисалы болуп I, 2, .., ''п''''','''... натуралдык сандардын катары эсептелет. А. п-нын мүчөлөрүнүн саны чектүү же чексиз болушу мүмкүн. Эгер А. п. . ''п'' мүчөдөн турса, анда анын мүчөлөрүнүн суммасы төмөнкү | Эгер ''d''>0 болсо, анда А. п. өсүүчү, эгер ''d''<0 болсо, кемүүчү деп аталат. А. п-нын эң жөнөкөй мисалы болуп I, 2, .., ''п''''','''... натуралдык сандардын катары эсептелет. А. п-нын мүчөлөрүнүн саны чектүү же чексиз болушу мүмкүн. Эгер А. п. . ''п'' мүчөдөн турса, анда анын мүчөлөрүнүн суммасы төмөнкү формула м-н чыгарылат: | ||
м-н чыгарылат: | |||
[[File:АРИФМЕТИКАЛЫК ПРОГРЕССИЯ_62.png | thumb | Формула 13]] | [[File:АРИФМЕТИКАЛЫК ПРОГРЕССИЯ_62.png | thumb | Формула 13]] | ||
12:24, 17 -ноябрь (Жетинин айы) 2022 -деги абалы
АРИФМЕТИКАЛЫК ПРОГРЕССИЯ (лат. progressio – өсүү) – сан удаалаштыгы, анын ар бир кийинки мүчөсү мурдакысына А. п-нын айырмасы деп аталган, кандайдыр d турактуу с анын кошуу м-н алынган сан катары. Ap бир А. п. . a,a+d,a+2d,a+3d,... түрүндө жазылат, жалпы мүчөсү ап = а + '(п -l) d. А. п-ны мүнөздөөчү формула :
Эгер d>0 болсо, анда А. п. өсүүчү, эгер d<0 болсо, кемүүчү деп аталат. А. п-нын эң жөнөкөй мисалы болуп I, 2, .., п,... натуралдык сандардын катары эсептелет. А. п-нын мүчөлөрүнүн саны чектүү же чексиз болушу мүмкүн. Эгер А. п. . п мүчөдөн турса, анда анын мүчөлөрүнүн суммасы төмөнкү формула м-н чыгарылат: