Difference between revisions of "АЯНТ (геометрия)"
м (Kadyrm moved page АЯНТ 1 to АЯНТ (геометрия) without leaving a redirect) |
|||
| 1 -сап: | 1 -сап: | ||
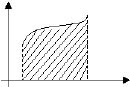
'''АЯНТ''' г е о м е т р и я д а ‒ 1) | '''АЯНТ''' г е о м е т р и я д а ‒ 1) геометриялык фигуралар <span cat='ж.кыск' oldv='м-н'>менен</span> беттердин сандык мүнөздөмөлөрүнүн бири. Аянт төмөнкү касиеттерге ээ: 1) терс эмес; 2) аддитивдүү; 3) жылдырууда сакталат; 4) бирдик квадраттын Аянты 1ге барабар. Аянтты эсептөө байыртадан эле геометриянын негизги маселелеринин бири болгон. Байыркы грек окумуштуулары айрым фигуралардын Аянттарын эсептөөнүн эрежелерин билишкен. Бул эрежелер Евклиддин «Башталыштар» аттуу жыйнагында теорема формасында берилген. Тегиздиктеги көп бурчтуктардын Аянттары көп бурчтуктарды тик бурчтуктарга келтирүү аркылуу ченелет. Айрым Аянттарды Кавальери принцибинин жардамы <span cat='ж.кыск' oldv='м-н'>менен</span> аныктоого болот. Ар кандай жалпак фигуралардын Аянттары аныкталган интегралдын жардамы <span cat='ж.кыск' oldv='м-н'>менен</span> эсептелинет. Мисалы, төмөн жагынан (''а,'' 0) <span cat='ж.кыск' oldv='ж-а'>жана</span> (''b,'' 0) арасындагы ''O<sub>x'' огунун кесиндиси <span cat='ж.кыск' oldv='м-н'>менен</span> чектелген, ал эми жогору жагынан терс эмес <span cat='ж.кыск' oldv='ж-а'>жана</span> [''a, b''] сегментинде аныкталган үзгүлтүксүз ''f(x'') функциясы <span cat='ж.кыск' oldv='м-н'>менен</span> чектелген фигуранын А-ты '''<math>S=\int_a^b f(x)\,dx</math>'''интегралы <span cat='ж.кыск' oldv='м-н'>менен</span> туюнтулат (к. сүрөт).<br>[[File:АЯНТ 190.png | thumb]]Көп грандыктын бетинин Аянты анын грандарынын Аянттарынын суммасына барабар.<math>\vec{r} = \vec{r} (u, v)</math> | ||
теӊдемеси <span cat="ж.кыск" oldv="м-н">менен</span> берилген ''D'' бетинин туюк аймагынын аянты төмөнкү формула <span cat="ж.кыск" oldv="м-н">менен</span> эсептелет:<math>\iint\limits_{(D)} \sqrt{g_{11} g_{22} - {g_{12}}^2} dudv</math>,мында <math>g_{11} = r_2^u,\qquad g_{12}=r_u r_v, \qquad g_{22} =r_2^v, </math> | теӊдемеси <span cat="ж.кыск" oldv="м-н">менен</span> берилген ''D'' бетинин туюк аймагынын аянты төмөнкү формула <span cat="ж.кыск" oldv="м-н">менен</span> эсептелет:<math>\iint\limits_{(D)} \sqrt{g_{11} g_{22} - {g_{12}}^2} dudv</math>,мында <math>g_{11} = r_2^u,\qquad g_{12}=r_u r_v, \qquad g_{22} =r_2^v, </math> | ||
10:19, 10 Январь (Үчтүн айы) 2024 -деги абалы
АЯНТ г е о м е т р и я д а ‒ 1) геометриялык фигуралар менен беттердин сандык мүнөздөмөлөрүнүн бири. Аянт төмөнкү касиеттерге ээ: 1) терс эмес; 2) аддитивдүү; 3) жылдырууда сакталат; 4) бирдик квадраттын Аянты 1ге барабар. Аянтты эсептөө байыртадан эле геометриянын негизги маселелеринин бири болгон. Байыркы грек окумуштуулары айрым фигуралардын Аянттарын эсептөөнүн эрежелерин билишкен. Бул эрежелер Евклиддин «Башталыштар» аттуу жыйнагында теорема формасында берилген. Тегиздиктеги көп бурчтуктардын Аянттары көп бурчтуктарды тик бурчтуктарга келтирүү аркылуу ченелет. Айрым Аянттарды Кавальери принцибинин жардамы менен аныктоого болот. Ар кандай жалпак фигуралардын Аянттары аныкталган интегралдын жардамы менен эсептелинет. Мисалы, төмөн жагынан (а, 0) жана (b, 0) арасындагы Ox огунун кесиндиси менен чектелген, ал эми жогору жагынан терс эмес жана [a, b] сегментинде аныкталган үзгүлтүксүз f(x) функциясы менен чектелген фигуранын А-ты интегралы менен туюнтулат (к. сүрөт).
Көп грандыктын бетинин Аянты анын грандарынын Аянттарынын суммасына барабар.
теӊдемеси менен берилген D бетинин туюк аймагынын аянты төмөнкү формула менен эсептелет:,мында ал эми rи жана rv болсо и жана v б-ча алынган жекече туундулар болот.
Б. Э. Канетов.