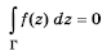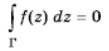Difference between revisions of "АНАЛИЗДИК ФУНКЦИЯ"
м (→top: clean up, replaced: м-н → <span cat='ж.кыск' oldv='м-н'>менен</span> (2), ж-а → <span cat='ж.кыск' oldv='ж-а'>жана</span> (6)) |
|||
| 1 -сап: | 1 -сап: | ||
'''АНАЛИЗДИК ФУНКЦИЯ''' – даражалуу катар түрүндө көрсөтүлүүчү функция. А. ф-лар теориясы комплекстик өзгөрмөлүү функциялар теориясы катары пайда болуп азыркы күндө да анын негизин түзөт. А. ф-лар теориясы XIX к-да түзүлүп, анын калыптанышына О. Коши, Б. Риман ж-а К. Вейерштрасстар көп салым кошкон. А. ф-лар классынын маанилүүлүгү төмөнкүлөр м-н аныкталат: 1) көлөмдүү, элементардык (көп мүчөлөр, рационалдык ж. б.) ж-а атайын функциялар (эллипстик, цилиндрлик ж. б.) кирет; 2) А. ф-лар классы арифметика, алгебра ж-а анализдин негизги амалдарына | '''АНАЛИЗДИК ФУНКЦИЯ''' – даражалуу катар түрүндө көрсөтүлүүчү функция. А. ф-лар теориясы комплекстик өзгөрмөлүү функциялар теориясы катары пайда болуп азыркы күндө да анын негизин түзөт. А. ф-лар теориясы XIX к-да түзүлүп, анын калыптанышына О. Коши, Б. Риман <span cat='ж.кыск' oldv='ж-а'>жана</span> К. Вейерштрасстар көп салым кошкон. А. ф-лар классынын маанилүүлүгү төмөнкүлөр <span cat='ж.кыск' oldv='м-н'>менен</span> аныкталат: 1) көлөмдүү, элементардык (көп мүчөлөр, рационалдык ж. б.) <span cat='ж.кыск' oldv='ж-а'>жана</span> атайын функциялар (эллипстик, цилиндрлик ж. б.) кирет; 2) А. ф-лар классы арифметика, алгебра <span cat='ж.кыск' oldv='ж-а'>жана</span> анализдин негизги амалдарына | ||
карата туюк, б. а. А. ф-ларга арифм. негизги | карата туюк, б. а. А. ф-ларга арифм. негизги | ||
амалдарды колдонгондо, анализдик коэфф-түү | амалдарды колдонгондо, анализдик коэфф-түү | ||
алг. тендемелерди чыгарганда ж-а аны дифференциалдаганда, интегралдаганда кайра эле А. ф-ны алабыз; 3) А. ф. орчундуу жалгыздык касиетине ээ: ар бир А. ф. «бир түйүндү» түзөт, өзүнүн жашоо облусунда «бирдиктүү» функция болот. Ал атайын функциялар теориясында, о. эле математиканын башка бөлүмдөрүндө, физикада, механикада, айрыкча гидродинамикада кеңири колдонулат. Эгер ''D'' облусунда аныкталган ''f(z)'' комплекстүү маанилүү функциясы | алг. тендемелерди чыгарганда <span cat='ж.кыск' oldv='ж-а'>жана</span> аны дифференциалдаганда, интегралдаганда кайра эле А. ф-ны алабыз; 3) А. ф. орчундуу жалгыздык касиетине ээ: ар бир А. ф. «бир түйүндү» түзөт, өзүнүн жашоо облусунда «бирдиктүү» функция болот. Ал атайын функциялар теориясында, о. эле математиканын башка бөлүмдөрүндө, физикада, механикада, айрыкча гидродинамикада кеңири колдонулат. Эгер ''D'' облусунда аныкталган ''f(z)'' комплекстүү маанилүү функциясы | ||
''z0eD'' чекитинин аймагында '''''f(z)=a0+a1(zz0)+...+an(z-z0)'<nowiki/>''Ч-..'''. даражалуу катары м-н аныкталса, анда ал z<sub>0</sub> чекитинде анализдик (голоморфтуу) деп аталат. ''D'' облусунун бардык чекиттеринде анализдик болгон функция бул облуста А. ф. болот. '''''z0sD''''' чекитинде А. ф. болсо бул чекитте дифференциаланат. '''''f(z)='' | ''z0eD'' чекитинин аймагында '''''f(z)=a0+a1(zz0)+...+an(z-z0)'<nowiki/>''Ч-..'''. даражалуу катары <span cat='ж.кыск' oldv='м-н'>менен</span> аныкталса, анда ал z<sub>0</sub> чекитинде анализдик (голоморфтуу) деп аталат. ''D'' облусунун бардык чекиттеринде анализдик болгон функция бул облуста А. ф. болот. '''''z0sD''''' чекитинде А. ф. болсо бул чекитте дифференциаланат. '''''f(z)='' | ||
=u(x,y)+iυ(x,y),''''' мында '''''z=x+iy''''' функциясы | =u(x,y)+iυ(x,y),''''' мында '''''z=x+iy''''' функциясы | ||
'''''z<sub>0</sub>ϵD''''' чекитинде А. ф. болсо, анда Коши – Риман шарты | '''''z<sub>0</sub>ϵD''''' чекитинде А. ф. болсо, анда Коши – Риман шарты | ||
аткарылат. А. ф. теориясында Кошинин интегралдык теоремасы чоң мааниге ээ: эгер ''f(z)'' функциясы ''D'' облусунда А. ф. болсо, анда ''D'' облусуна тиешелүү болгон каалаган облусту чектеген ''Г'' туюк ийри сызыгы үчүн<br> | аткарылат. А. ф. теориясында Кошинин интегралдык теоремасы чоң мааниге ээ: эгер ''f(z)'' функциясы ''D'' облусунда А. ф. болсо, анда ''D'' облусуна тиешелүү болгон каалаган облусту чектеген ''Г'' туюк ийри сызыгы үчүн<br> | ||
[[File:АНАЛИЗДИК ФУНКЦИЯ_58.png | thumb | Formula.F2]] | [[File:АНАЛИЗДИК ФУНКЦИЯ_58.png | thumb|Formula.F2]] | ||
деп жазылат. Буга тескери теорема да орун алат: эгер ''f(z)'' функциясы | деп жазылат. Буга тескери теорема да орун алат: эгер ''f(z)'' функциясы | ||
''D'' облусунда үзгүлтүксүз ж-а каалагандай '''''Г ⸦ D'''''<br> | ''D'' облусунда үзгүлтүксүз <span cat='ж.кыск' oldv='ж-а'>жана</span> каалагандай '''''Г ⸦ D'''''<br> | ||
туюк контур үчүн <br> | туюк контур үчүн <br> | ||
<br> | <br> | ||
[[File:АНАЛИЗДИК ФУНКЦИЯ_59.png | thumb | Formula.F3]] | [[File:АНАЛИЗДИК ФУНКЦИЯ_59.png | thumb|Formula.F3]] | ||
болсо, анда ''f(z)'' функциясы ''D'' облусунда А. ф. болот (Морера теоремасы). <br> | болсо, анда ''f(z)'' функциясы ''D'' облусунда А. ф. болот (Морера теоремасы). <br> | ||
[[File:АНАЛИЗДИК ФУНКЦИЯ_60.png | thumb | Formula.F4]] | [[File:АНАЛИЗДИК ФУНКЦИЯ_60.png | thumb|Formula.F4]] | ||
''zϵD'' Кошинин интегралдык формуласы. ''D'' облусунда анализдик ж-а бул облуста пределдик чекитке ээ болгон кандайдыр бир көптүктө бири бирине дал келүүчү эки функция бүт ''D'' облусунда бири бирине дал келет. Айрым алганда, нөлдөн айырмаланган ''D'' облусунда ал обочолонгон нөлдөргө гана ээ болушу мүмкүн. А. ф-нын аналитикалуулугу бузулган чекиттери өзгөчө чекиттер деп аталат. Бүт тегиздиктеги А. ф. бүтүн функция деп аталат.<br> | ''zϵD'' Кошинин интегралдык формуласы. ''D'' облусунда анализдик <span cat='ж.кыск' oldv='ж-а'>жана</span> бул облуста пределдик чекитке ээ болгон кандайдыр бир көптүктө бири бирине дал келүүчү эки функция бүт ''D'' облусунда бири бирине дал келет. Айрым алганда, нөлдөн айырмаланган ''D'' облусунда ал обочолонгон нөлдөргө гана ээ болушу мүмкүн. А. ф-нын аналитикалуулугу бузулган чекиттери өзгөчө чекиттер деп аталат. Бүт тегиздиктеги А. ф. бүтүн функция деп аталат.<br> | ||
Ад.: ''СидоровЮ.В., Федерюк М.В., Шабунин'' М. И. Лекции по теории функций комплексного переменного. М.: 1989; ''Шабат Б. В.'' Введение в комплексный анализ. М., 1969; ''Бицадзе А. В.'' Основы теории аналитических функций комплексного переменного. М., 1969. <br> | Ад.: ''СидоровЮ.В., Федерюк М.В., Шабунин'' М. И. Лекции по теории функций комплексного переменного. М.: 1989; ''Шабат Б. В.'' Введение в комплексный анализ. М., 1969; ''Бицадзе А. В.'' Основы теории аналитических функций комплексного переменного. М., 1969. <br> | ||
Б.Э. Сулайманов. | Б.Э. Сулайманов. | ||
16:50, 5 Декабрь (Бештин айы) 2022 -деги абалы
АНАЛИЗДИК ФУНКЦИЯ – даражалуу катар түрүндө көрсөтүлүүчү функция. А. ф-лар теориясы комплекстик өзгөрмөлүү функциялар теориясы катары пайда болуп азыркы күндө да анын негизин түзөт. А. ф-лар теориясы XIX к-да түзүлүп, анын калыптанышына О. Коши, Б. Риман жана К. Вейерштрасстар көп салым кошкон. А. ф-лар классынын маанилүүлүгү төмөнкүлөр менен аныкталат: 1) көлөмдүү, элементардык (көп мүчөлөр, рационалдык ж. б.) жана атайын функциялар (эллипстик, цилиндрлик ж. б.) кирет; 2) А. ф-лар классы арифметика, алгебра жана анализдин негизги амалдарына карата туюк, б. а. А. ф-ларга арифм. негизги амалдарды колдонгондо, анализдик коэфф-түү алг. тендемелерди чыгарганда жана аны дифференциалдаганда, интегралдаганда кайра эле А. ф-ны алабыз; 3) А. ф. орчундуу жалгыздык касиетине ээ: ар бир А. ф. «бир түйүндү» түзөт, өзүнүн жашоо облусунда «бирдиктүү» функция болот. Ал атайын функциялар теориясында, о. эле математиканын башка бөлүмдөрүндө, физикада, механикада, айрыкча гидродинамикада кеңири колдонулат. Эгер D облусунда аныкталган f(z) комплекстүү маанилүү функциясы z0eD чекитинин аймагында f(z)=a0+a1(zz0)+...+an(z-z0)'Ч-... даражалуу катары менен аныкталса, анда ал z0 чекитинде анализдик (голоморфтуу) деп аталат. D облусунун бардык чекиттеринде анализдик болгон функция бул облуста А. ф. болот. z0sD чекитинде А. ф. болсо бул чекитте дифференциаланат. f(z)= =u(x,y)+iυ(x,y), мында z=x+iy функциясы z0ϵD чекитинде А. ф. болсо, анда Коши – Риман шарты
аткарылат. А. ф. теориясында Кошинин интегралдык теоремасы чоң мааниге ээ: эгер f(z) функциясы D облусунда А. ф. болсо, анда D облусуна тиешелүү болгон каалаган облусту чектеген Г туюк ийри сызыгы үчүн
деп жазылат. Буга тескери теорема да орун алат: эгер f(z) функциясы
D облусунда үзгүлтүксүз жана каалагандай Г ⸦ D
туюк контур үчүн
болсо, анда f(z) функциясы D облусунда А. ф. болот (Морера теоремасы).
zϵD Кошинин интегралдык формуласы. D облусунда анализдик жана бул облуста пределдик чекитке ээ болгон кандайдыр бир көптүктө бири бирине дал келүүчү эки функция бүт D облусунда бири бирине дал келет. Айрым алганда, нөлдөн айырмаланган D облусунда ал обочолонгон нөлдөргө гана ээ болушу мүмкүн. А. ф-нын аналитикалуулугу бузулган чекиттери өзгөчө чекиттер деп аталат. Бүт тегиздиктеги А. ф. бүтүн функция деп аталат.
Ад.: СидоровЮ.В., Федерюк М.В., Шабунин М. И. Лекции по теории функций комплексного переменного. М.: 1989; Шабат Б. В. Введение в комплексный анализ. М., 1969; Бицадзе А. В. Основы теории аналитических функций комплексного переменного. М., 1969.
Б.Э. Сулайманов.