Difference between revisions of "АРАЛАШ КӨБӨЙТҮНДҮ"
Jump to navigation
Jump to search
Tags: Reverted Визуалдык редактор |
Tag: Reverted |
||
| 5 -сап: | 5 -сап: | ||
- (\vec{b}, \vec{a}, \vec{c}) = | - (\vec{b}, \vec{a}, \vec{c}) = | ||
- (\vec{a}, \vec{c}, \vec{b}) = | - (\vec{a}, \vec{c}, \vec{b}) = | ||
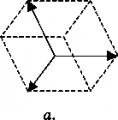
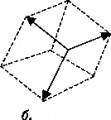
- (\vec{c}, \vec{b}, \vec{a}), (\vec{a}, \vec{b}, \vec{c}) = 0 </math>. Компланардуу эмес <math display="inline">\vec{a}, \vec{b}, \vec{c}</math> векторлорунун А. к-сү ал векторлор аркылуу тургузулган оң же терс белгиде алынган параллелепипеддин көлөмүнө барабар: <math display="inline">V = \pm (\vec{a}, [\vec{b}, \vec{c}])</math>'''''.''''' Эгер <math display="inline">\vec{a}, \vec{b}, \vec{c}</math> векторлору оң үчүлтүктү түзсө, анда көлөм ''V'' оң (+) белги м-н ''(а,'' сүрөт), ал эми | - (\vec{c}, \vec{b}, \vec{a}), (\vec{a}, \vec{b}, \vec{c}) = 0 </math>. Компланардуу эмес <math display="inline">\vec{a}, \vec{b}, \vec{c}</math> векторлорунун А. к-сү ал векторлор аркылуу тургузулган оң же терс белгиде алынган параллелепипеддин көлөмүнө барабар: <math display="inline">V = \pm (\vec{a}, [\vec{b}, \vec{c}])</math>'''''.''''' Эгер <math display="inline">\vec{a}, \vec{b}, \vec{c}</math> векторлору оң үчүлтүктү түзсө, анда көлөм ''V'' оң (+) белги м-н ''(а,'' сүрөт), ал эми | ||
<gallery> | <gallery> | ||
File:АРАЛАШ КӨБӨЙТҮНДҮ_36.png | File:АРАЛАШ КӨБӨЙТҮНДҮ_36.png | ||
| 18 -сап: | 18 -сап: | ||
\\ Z_1 & Z_2 & Z_3 | \\ Z_1 & Z_2 & Z_3 | ||
\end{vmatrix} </math>'' | \end{vmatrix} </math>'' | ||
''Б. Э. Канетов.''<br> | ''Б. Э. Канетов.''<br> | ||
22:47, 16 -ноябрь (Жетинин айы) 2022 -деги абалы
АРАЛАШ КӨБӨЙТҮНДҮ – вектору м-н ж-а векторлорунун вектордук көбөйтүндүсүнүн скалярдык көбөйтүндүсү: = . А. к. төмөнкү касиеттерге ээ: эгер = 0, же = 0, же = 0 же векторлору компланардуу болсо . Компланардуу эмес векторлорунун А. к-сү ал векторлор аркылуу тургузулган оң же терс белгиде алынган параллелепипеддин көлөмүнө барабар: . Эгер векторлору оң үчүлтүктү түзсө, анда көлөм V оң (+) белги м-н (а, сүрөт), ал эми
сол үчүлтүктү түзсө, көлөм V терс (-) белги м-н алынат (б, сүрөт). Эгер векторлору
{X1, X2, X3}, { Y1, Y2, Y3}, { Z1, Z2, Z3} координаталарына ээ болсо, анда ,
Б. Э. Канетов.




![{\textstyle ({\vec {a}},[{\vec {b}},{\vec {c}}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cd14ac4f6cd6b56c81ec04362a0ee4060171aad)


![{\textstyle V=\pm ({\vec {a}},[{\vec {b}},{\vec {c}}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/949a8532ad98aa7c26c9a9eeb465997cf7bafe33)