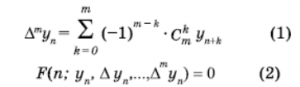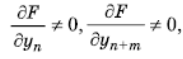АЙЫРМАЛЫК ТЕҢДЕМЕ

изделүүчү функ­циянын чектүү айырмасын камтыган теңдеме. Failed to parse (syntax error): {\displaystyle У(п) = у_п(п ='' 0, ±1, ±2,...)''} бүтүн сандуу аргу­менттүү функция;

Failed to parse (syntax error): {\displaystyle Ау_п ='' г/_п+1 – г/_п_ ''А^т+1у_п = ҢА^ту_п),} Failed to parse (syntax error): {\displaystyle &^гу_п = Ду_п, т = } 1, 2, ... чектүү айырмалар болсо, ∆^mу_n туюнтмасы у функциясынын (m+1) чеки­тинде п, n+1, ..., п+т маанилерине ээ болуп, төмөнкү формула алынат:

$\Delta ^{m}y_{n}=\sum _{k=0}^{m}(-1)^{m-k}\bullet C_{m}^{k}y_{n+k}$     (1)

$F(n;y_{n},\Delta y_{n},...,\Delta ^{m}y_{n})=0$      (2)

Формула. 1

түрүндөгү теңдеме А. т. деп аталат, мында у ­изделүүчү, F – берилген функция. (2)де чектүү айырмаларды алардын туюнтмалары м‑н (1) теңдемеге ылайык изделүүчү функциялардын маанилери аркылуу алмаштырса, анда төмөнкүдөй теңдеме алынат:

$F(n;y_{n},y_{n+1},...,y_{n+m})=0.$     (3)

Формула. 2

Эгер

${\partial F \over \partial y_{n}}\neq 0,{\partial F \over \partial y_{n}}\neq 0,$

Формула. 3

(3) тендемеде чынын- да эле у_п да, у_п+m да бар болсо, анда (3) тендеме ­тартиптеги А. т. же дифференциал – А. т. деп аталат. А. т‑ге келтирилүүчү мат. ж‑а тех. мо­делдер бар болсо да, анын негизги колдонулуу­чу аймагы дифференциалдык теңдемелерди жа­кындаштырып чыгаруу ыкмалары болуп эсеп­телет. Б. К. Темиров.